表面张力是钢液的重要物理性质之一，对于钢材洁净度控制及凝固成型过程均具有重要影响。钢液表面层和内部粒子所处的环境不同，两者所受的力并不相同，使钢液表面产生自发缩小倾向的力称为钢液的表面张力。钢液的表面张力不仅对新相的生成有影响，而且对相间反应、渣钢分离、钢液对耐火材料的侵蚀等也产生影响，准确获取钢液的表面张力对于优化冶炼过程、改善钢材质量、提升生产效率具有重要意义。

目前，表面张力主要通过实验测定方法获得，对于液态金属，常用的是气泡最大压力法和静滴法。影响钢液表面张力的因素众多，主要包括钢液成分、温度及钢液的接触环境，对于钢液来说，温度通常在1700K以上，一方面，高温条件的稳定获得难度较高，即温度精确控制难度较高，对表面张力的测定精度存在影响，另一方面，高温钢液极易与接触介质发生反应，即钢液成分难以稳定控制，测得的表面张力易于偏离真实值；再者，真实钢液组元复杂，各组元对表面张力的交互影响难以充分分离；另外，钢液表面张力高温测定还存在流程复杂、成本高等不足。

近年来，随着计算机硬件及计算机数值模拟技术快速发展，其中分子动力学(MD)是一种利用牛顿运动定律模拟原子或分子系统的强大方法，可从微观尺度解析物理化学过程，目前已成为研究材料微观结构和性能的有效方法，在高温冶金熔体领域应用也逐渐扩展。

鉴于现有表面张力获取技术存在的不足，东北大学闵义团队供一种采用模拟计算获取钢液面张力的方法，即采用分子动力学模拟的方法计算钢液原子尺度的微观结构信息，并以此为基础获取不同成分、温度条件下钢液的表面张力，该方法可有效避免传统高温实验测定方法的数据波动大、影响因素难以分离及成本高等问题；另外，本方法基于钢液的微观结构信息获得表面张力，可深化对表面张力产生本质的理解及影响因素的解析，对于钢液表面张力控制可提供明确指导。

Fe-C二元体系-真空基于微观结构解析的钢液表面张力计算方法：

(1)根据冶金钢液的主要化学成分，钢液由Fe-C二元体系组成，具体成分为Fe：99.85％，C：0.15％。

(2)Fe-C二元体系的原子数设定为12000个，根据Fe-C二元体系中各组分的摩尔比，可确定不同原子的个数，之后再根据Fe-C二元体系在高温液态条件下的密度，可计算出模拟盒子的边长，具体如表1所示。

表1Fe-C二元体系的原子数、密度和盒子边长

基于表2中的原子种类、个数及Fe-C二元体系的密度，采用Materials Studio软件建立Fe-C二元体系的初始结构模型，得到一个包含原子数目、原子类型数目、各类型原子质量、原子ID及该原子ID所对应的原子类型和x、y、z三个方向的坐标值的初始结构data文件。

(3)选取改进嵌入原子法(MEAM)作为描述Fe-C二元体系中所有原子间相互作用力的势函数。

(4)设置模拟计算的参数，编写执行LAMMPS软件分子动力学模拟计算所需的in文件，将建立的Fe-C二元体系初始结构模型信息导入LAMMPS软件进行分子动力学模拟计算。原子类型设置为atomic，采用周期性边界条件，整个模拟过程使用正则系综(NVT)，模拟过程中原子数、体积和温度不变，采用Parrinello-Rahman法和Nose-Hoover热浴法进行压力和温度的控制。根据高斯速度分布给出了铁原子的初始速度分布。体系的牛顿运动方程的数值解法采用Verlet算法进行求解，步长设置为1fs，每1000步保存一次数据，一共运行510000步。首先在初始温度为4273K下运行60000步，采用共轭梯度法使初始结构的能量最小化，使体系充分混合及能量稳定。接下来，通过100000个时间步长使体系降温到1950K，并在1950K下继续弛豫50000步。沿z轴方向在盒子的两侧加入两个真空区，形成平行于z轴方向的真空-液体-真空夹层结构，对扩大后的系统在1950K下弛豫300000步，为了防止液膜的游走，在每个MD步骤中都要调整系统的质心位于系统的中心，并在此阶段收集计算微观结构信息和表面张力所需的数据，最后得到模拟体系的原子坐标文件、压力张量等模拟结果数据。

(5)将得到的原子坐标文件导入OVITO、VESTA和VMD软件中进行可视化分析并计算模拟体系的微观结构信息，得到模拟体系的微观结构图；计算表面张力所需数据收集前后模拟体系的微观结构，将各个类型的原子进行区分，计算出不同原子对之间的径向分布函数；根据计算得到的径向分布函数第一峰横坐标值得出不同原子对之间的键长(最近邻距离)，将径向函数的第一峰进行积分可得出不同原子对之间的配位数。可导出模拟盒子不同区域的原子坐标文件用于微观结构信息计算。

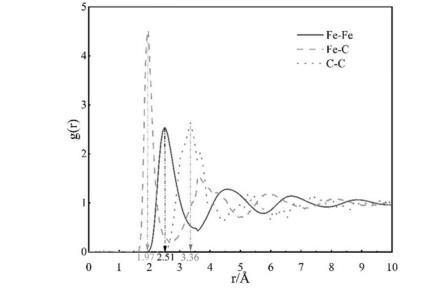
Fe-C二元体系经计算得到的径向分布函数，Fe-Fe、Fe-C、C-C原子对的平均键长分别为若原子间距离小于相应的键长值则表示两个原子之间互相连接，根据碳原子连接的铁原子个数，可将铁原子区分为自由态铁原子(与碳原子没有配位关系)、A型铁(只与1个碳原子形成配位关系)、B型铁(与2个或更多的碳原子形成配位关系)三种类别，根据模拟结果数据可对铁原子的配位方式进行分析。

(6)根据收集的计算表面张力所需的数据，采用此钢液表面张力计算方法计算Fe-C二元体系的表面张力。计算得到的法向压力张量和和切向压力张量之差PN-PT、表面张力σ和密度ρ沿z轴的分布，Fe-C二元体系的表面张力σ经计算为1.531N/m。

小结

根据压力张量与表面张力的关系，提供了一种从原子尺度预测计算钢液表面张力的方法，可获取不同成分和温度条件下钢液的表面张力，可有效避免传统高温实验测定影响因素难以分离、流程复杂及成本高等问题，可用于填补实验数据的空白；结合钢液的微观结构信息，可对钢液表面张力进行微观结构解析，从而为钢液表面张力的控制提供理论指导。