密度梯度理论中仅需要“影响因子”一个参数即可，该参数的理论计算方法复杂、计算程序繁琐，因此通用的方法是由纯物质的表面张力数据回归得到纯物质的影响因子，该方法已广泛用于表面张力的预测。密度梯度理论与状态方程结合计算表面张力，可选择不同的状态方程，如立方型状态方程、流体缔合理论(StatisticAssociatingFluidTheory，SAFT)状态方程等，由于立方型状态方程形式简单、通用性好，因此，立方型方程与密度梯度理论结合计算表面张力得到很大的发展和研究。

密度梯度理论物理意义清晰、理论形式相对简单，能够成功地应用于纯物质界面性质的描述，比较容易推广到混合物体系计算。但目前研究中存在一些问题：很多研究中获得的影响因子往往只针对某一类物质，或者仅以列表形式给出文中涉及物质的影响因子，通用性差；SAFT方程形式复杂，需要实验数据回归方程参数，无法以此建立简单通用的计算模型，并且该方程与密度梯度理论结合计算表面张力的预测结果不是很好。因此，通用的影响因子计算公式的提出对该理论用于表面张力计算的研究具有非常重要的指导意义。

本研究采用PR[7]状态方程与密度梯度理论结合计算表面张力。PR状态方程的原始表达式如方程(8)-(13)所示，1978年Robinson和Peng[8]对原始的PR方程进行了修订，偏心因子ω＞0.49时，m值由方程(13)得到

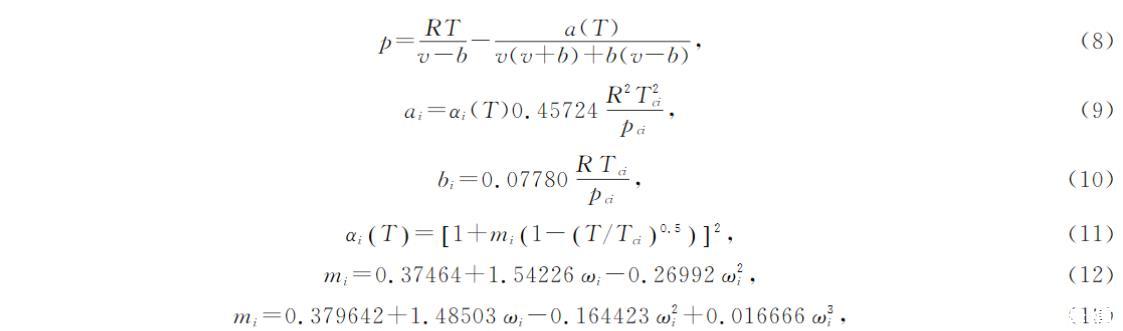
p＝RT/(v－b)－a(T)/[v(v＋b)＋b(v－b)]， (8)

ai＝αi(T)0.45724R²Tc²i/pci， (9)

bi＝0.07780RTci/pci， (10)

αi(T)＝[1＋mi(1－√(T/Tci))]²， (11)

mi＝0.37464＋1.54226ωi－0.26992ω²i， (12)

mi＝0.379642＋1.48503ωi－0.164423ω²i＋0.016666ω³i， (13)

式中p为平衡压力，单位是Pa；R为理想气体常数，单位是J/mol/K；T为温度，单位是K；v为摩尔体积，单位是m³/mol；Tc为临界温度，单位是K；Pc为临界压力，单位是Pa；ω为偏心因子。

2 计算模型

本研究共收集整理了碳原子数在6-24之间的脂肪酸酯，通过查阅文献实验数据，对文献数据进行分析整理，分类总结。共整理了19种不同碳数、不同双键数的脂肪酸酯的209个表面张力实验数据，温度范围为283.15-373.15K。采用方程(7)计算得到脂肪酸酯类影响因子C的实验值，分析影响因子随温度和碳碳双键数的变化规律，提出脂肪酸酯类影响因子的关联式(如方程(14)所示)，采用最小二乘法进行非线性拟合回归，目标函数(ObjectiveFunction-OF)如方程(15)所示，计算结果如表2所示，详细的计算结果见附录，全部数据用于回归拟合时，方程(14)的统计参数R²和AARD分别为0.9892和1.50%。

影响因子实验值与计算值比较如图1所示，由图1可知，所有的数据点几乎都落在中间对角线上，影响因子计算值与实验测定值一致性很好，说明该模型可精确的估算脂肪酸酯类的表面张力。影响因子关联式误差分布如图2所示，由图2可知，相对误差RD%绝大部分小于2%，说明计算结果较好。

C＝p1＋p2∗ln(T)＋p3∗(ln(T))²＋p4∗(ln(T))³＋p5∗(Z)/(1＋p6∗ln(T)＋p7∗Z)， (14)

式中C为影响因子；T为温度，K；Z为碳碳双键数；p1、p2、p3、p4、p5、p6、p7为回归参数，参数值如表1所示。

OF＝min∑(yexp-ycal)²， (15)

式中yexp和ycal分别为影响因子实验值和计算值。

AARD%＝∑(γexp.－γcal.

/γexp.)×100/n， (16)

RD%＝(γexp.－γcal.

/γexp.)×100。 (17)

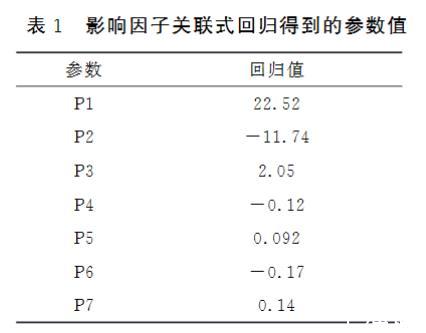
表1 影响因子关联式回归得到的参数值

参数 回归值

P1 22.52

P2 -11.74

P3 2.05

P4 -0.12

P5 0.092

P6 -0.17

P7 0.14

为进一步检测提出模型的预测能力，本文采用外推验证(ExternalValidation)评估新模型。将所有数据随机分为试验集(159)和测试集(50)，训练集用于重新回归关联方程(14)的参数，新得到的参数用于计算测试集的表面张力值，训练集和测试集的计算结果如表2所示。试验集的R²＝0.9842，AARD＝1.40%，测试集的R²＝0.9951，AARD＝0.76%，由表2可以看到，训练集的统计参数R²和AARD与所有数据参与回归时得到的统计参数几乎一致。

表2 模型计算结果

模型 数据量 R² AARD

全部 209 0.9892 1.50%

试验集 159 0.9842 1.40%

测试集 50 0.9951 0.76%

以上结果表明，该模型估算脂肪酯类的表面张力值具有很好的预测能力。

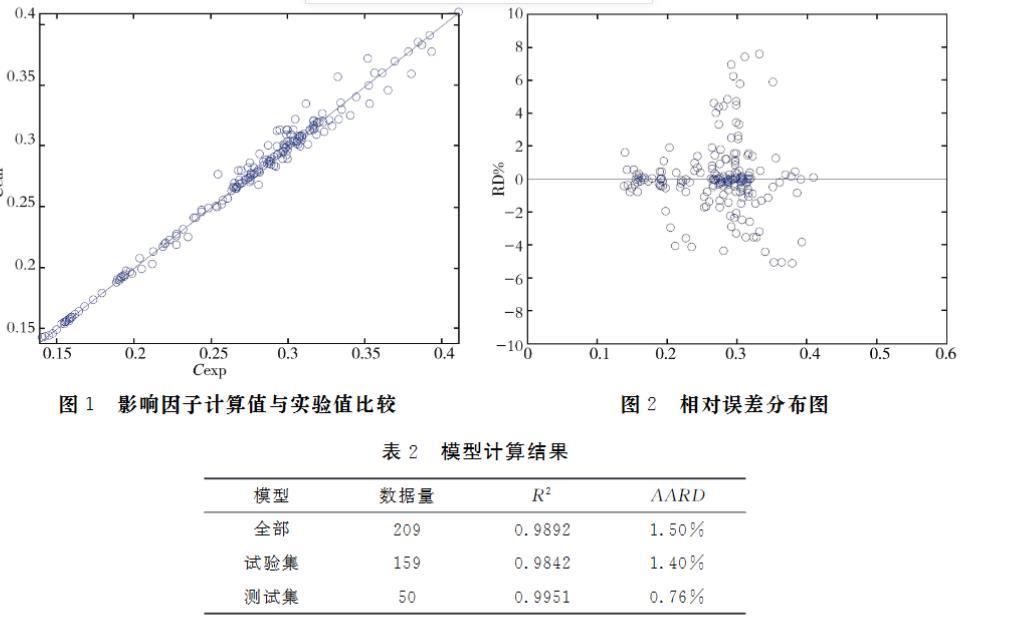
图1 影响因子计算值与实验值比较

图2 相对误差分布图

结论

分析和讨论了温度和碳碳双键数对脂肪酸酯表面张力的影响，整理了现有文献中脂肪酸酯的表面张力实验值，将密度梯度理论与PR状态方程结合，分析影响因子随温度和碳碳双键数的变化规律，提出了表面张力的关键参数-影响因子的关联式。该关联式的统计参数R²和AARD分别为0.9892和1.50%，并对该关联式进行了外推验证，试验集的R²＝0.9842，AARD＝1.40%，测试集的R²＝0.9951，AARD＝0.76%，训练集的统计参数R²和AARD与所有数据参与回归时得到的统计参数几乎一致。以上数据表明该关联式的预测能力较好。