合作客户/
拜耳公司 |
同济大学 |
联合大学 |
美国保洁 |
美国强生 |
瑞士罗氏 |
相关新闻Info
推荐新闻Info
-
> 氢氧化钠用量对重烷基苯磺酸钠水溶液/油体系界面张力的影响(二)
> 氢氧化钠用量对重烷基苯磺酸钠水溶液/油体系界面张力的影响(一)
> 3种不同变质煤样经湿法超细粉碎后煤颗粒表面张力变化(二)
> 3种不同变质煤样经湿法超细粉碎后煤颗粒表面张力变化(一)
> 全自动表面张力仪在铅锌矿悬浮液雾化效率分析中的应用(二)
> 全自动表面张力仪在铅锌矿悬浮液雾化效率分析中的应用(一)
> 微通道流动沸腾中表面张力的关键作用机制研究(三)
> 微通道流动沸腾中表面张力的关键作用机制研究(二)
> 微通道流动沸腾中表面张力的关键作用机制研究(一)
> 电场电压对明胶液滴荷质比、表面张力的影响及预测模型构建(三)
电镀液表面张力、接触角、流速以及压强等因素对硅通孔浸润过程的影响(二)
来源:《复旦学报(自然科学版)》 浏览 462 次 发布时间:2025-11-26
3流速的影响
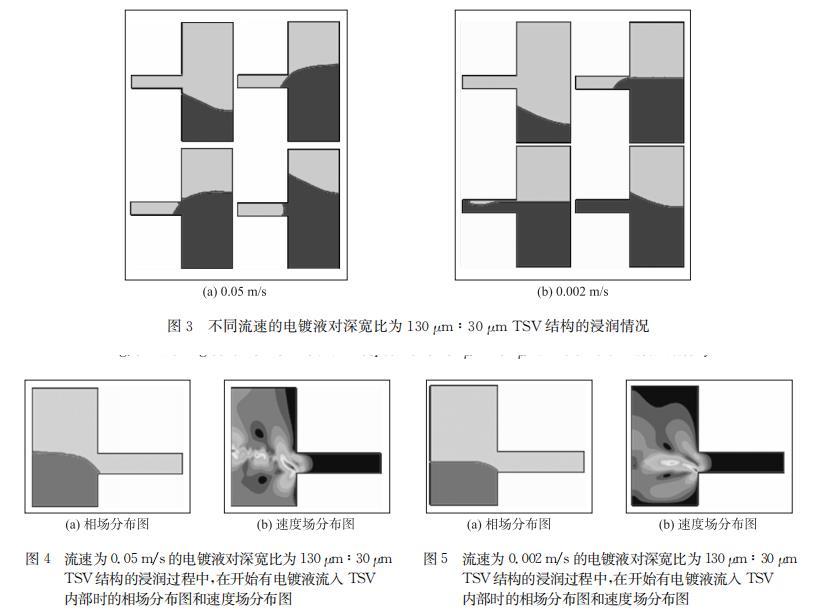
TSV深宽比设置为130μm:30μm,电镀液流人速度为0.05 m/s和0.002 m/s的浸润仿真结果分别如图3所示,前者在TSV底部形成气泡,后者可以完全浸润。模拟结果表明降低电镀液流入速度有利于浸润。通过仿真中两种情况下浸润过程中的流速场对比,可以看出在电镀液流入的过程中,电镀液流人速度较大时,如图4(b)所示,电镀液表面距离TSV较远的部分有着相对更大的流速,即电镀液流过TSV上方的速度大于电镀液向TSV内部流入的速度,导致在电镀液流过TSV上方时,其流入TSV内部的分流量还没有充满TSV内部排出其中气体之前,电镀液就已经流过了TSV上方,并将TSV口部封死,导致内部残留气体无法排出,形成不完全浸润;而当电镀液流入速度较小时,如图5(b)所示,电镀液表面在TSV口部附近具有相对更大的流速,即电镀液向TSV内部流入的速度大于其流过TSV上方的速度,使得电镀液流过TSV上方时,有足够的分流量流入TSV内部,将其中气体排出并将TSV填满,实现完全的浸润。
但是按照同样设置仿真了流速为0.002 m/s时,深宽比为120μm:20μm的情况,结果为不可完全浸润,这说明通过控制流速的方法促进浸润的效果是有限的,还需要进一步讨论更有效的方法。
4表面张力和接触角的影响
电镀液的表面张力和接触角都会对浸润结果产生影响,为明确这些影响对浸润的具体效果,首先使用JK99B型全自动张力仪对表面张力和接触角进行了测定,测量结果在表1中分别列出。由测量数据可以发现,随着活性剂的增多,表面张力下降很明显,而接触角随着活性剂的增多没有显著的减小;表面张力和接触角都在减小到一定程度之后趋于稳定。
表1电镀液与空气之间的表面张力和与样片表面(表面为铜种子层)的接触角
| 被测溶液 | 表面张力(mN/m) | 接触角(°) |
|---|---|---|
| 纯水 | 74.875 | 83.79 |
| TSV标准镀液 | 59.542 | 64.44 |
| TSV标准镀液1L中加入2mL活性剂溶液 | 46.458 | 59.59 |
| TSV标准镀液1L中加入5mL活性剂溶液 | 43.292 | 57.60 |
| TSV标准镀液1L中加入10mL活性剂溶液 | 34.333 | 56.34 |
| TSV标准镀液1L中加入20mL活性剂溶液 | 27.792 | 52.91 |
| 纯活性剂溶液 | 26.208 | 50.06 |
注:活性剂溶液平配比为100g水:0.1g十二烷基磺酸。
根据实际测定结果,按照图1所示的相应边界条件建立表面张力与接触角不同的三种模型,其中TSV的深宽比均为120μm:20μm,电镀液从边界1以0.002 m/s的速度流入,空气设置为理想不可压气体,三组模型的具体参数设置和仿真结果分别见表2和图6。
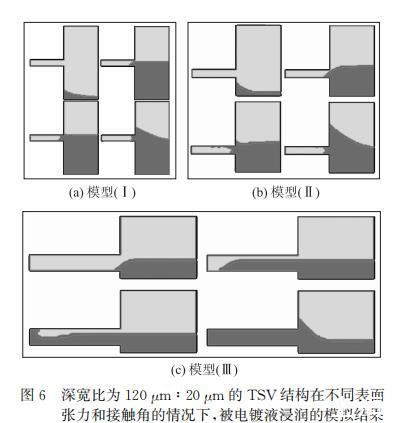
模型(I)使用的表面张力和接触角为不含活性剂的TSV标准镀液的实际测量值,仿真结果是不能完全浸润;模型(II)采用的是在1L TSV标准镀液中加入20mL活性剂溶液的实际测量值,这两种模型在仿真中均表现为不能完全浸润。
以上降低表面张力和接触角的方法都是通过添加表面活性剂来改变电镀液的性质,而实际中可以通过改变固体样品表面的性质来降低固液界面处的参数接触角,故将模型(III)仅仅设置为将模型(II)中的接触角减小为40°,其他条件均不变化,仿真结果是可以完全浸润。并且,在考虑润湿性优劣方面,主要参数为接触角,故仿真结果表明通过改变固体样片表面性能来减小电镀液在样片表面的接触角是实现优化浸润结果的一种非常有效的方法。
| 模型编号 | 表面张力(mN/m) | 接触角(°) |
|---|---|---|
| (I) | 64.44 | 64 |
| (II) | 27.792 | 52 |
| (III) | 27.792 | 40 |
5压强的影响
在考虑压强对浸润效果的影响时,和上述模型最显著的不同就是要将理想不可压气体改成理想可压气体。因为通过改变TSV结构所处环境的压强来优化浸润效果的过程中必然涉及到液体对空气的压缩,即仿真中空气的密度参数是一个可变的值。但是这一改变会使得达到收敛计算更加困难;并且这里必须要考虑Fluent软件计算能达到的真空程度。
Fluent中都是用连续介质模型处理才能得到计算结果。连续介质模型是将流体介质的一些物理属性如密度压强速度等都看作是空间及时间的可微连续函数。其成立条件是流体平均自由程远远小于物体特征尺寸,即:Lgglambda。
本文中这部分模型中的特征尺寸L为:20μm。
流体空气的平均自由程lambda计算公式如下:

其中,V:空气分子一秒钟内的平均路程,Z:空气分子1秒钟的平均碰撞次数,d:空气分子直径,P为TSV所处环境的压强。
根据公式Lgglambda,Fluent所能模拟的压强最低的数量级为103。因此做三组对比仿真,考虑到深宽比较大时迭代步长需设置的很小,导致仿真时间很长,故TSV的深宽比均设为150μm:50μm,TSV结构所处环境压强分别设为10^5 Pa、10^4 Pa和3000 Pa。仿真结果如图7所示,当压强为10^5 Pa时,TSV底部残留非常大的气泡;当压强为10^3 Pa时,TSV底部残留较小气泡;当压强为3000 Pa时,可以基本浸润。
6影响因素的仿真结果总结
表3、表4、表5为上述针对不同影响因素进行的模拟仿真结果总结。
| 流速(m/s) | TSV深宽比2) | |||
|---|---|---|---|---|
| 150μm:75μm | 150μm:50μm | 130μm:30μm | 120μm:20μm | |
| 0.05 | 完全浸润 | 不能完全浸润 | 不能完全浸润 | 不能完全浸润 |
| 0.002 | 完全浸润 | 完全浸润 | 完全浸润 | 不能完全浸润 |
| 表面张力(mN/m)、接触角(°) | TSV深宽比 | |||
|---|---|---|---|---|
| 150μm:75μm | 150μm:50μm | 130μm:30μm | 120μm:20μm | |
| 27.792、52 | 完全浸润 | 完全浸润 | 完全浸润 | 不能完全浸润 |
| 27.792、40 | 完全浸润 | 完全浸润 | 完全浸润 | 完全浸润 |
| 压强(Pa) | 浸润情况 |
|---|---|
| 105 | TSV底部残留非常大的气泡 |
| 104 | TSV底部残留较小气泡 |
| 3000 | 基本浸润 |
上述Fluent软件和相关实验对电镀液浸润TSV的研究表明,当TSV结构的深宽比大于2的时候,没有经过预润湿而直接放入电镀液的TSV结构很难实现无空洞电镀填充。电镀液与空气之间的表面张力较小,电镀液与待电镀样片表面的接触角约为40°左右时,可对深宽比低于或等于120μm:20μm的TSV实现完全浸润;浸润过程中电镀液的流速为0.002 m/s时即可对深宽比低于或等于130μm:30μm的TSV实现完全浸润;浸润所处环境的压强低于3000 Pa时即可在流速为0.05 m/s时对深宽比为150μm:50μm的TSV基本实现完全浸润。










